Aufgabe B 1
Ein Künstler teilt einen quaderförmigen Container durch einen ebenen Schnitt
in einen großen und einen kleinen Teilkörper.
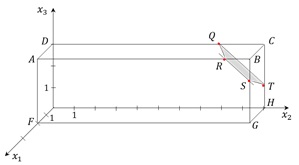
Der Container wird in einem Koordinatensystem als Quader mit den Eckpunkten
A(2|0|3), B(2|10|3), C(0|10|3), D, F, G(2|10|0), H und O(0|0|0) dargestellt
(Koordinatenangaben in Meter).
Die Ebene E scheidet die Kanten des Quaders in den Punkten R(2|9|3), S(2|10|2),
T(0|10|1) und Q(0|8|3).
Der kleine Teilkörper hat also die Eckpunkte Q, R, S, T, B, C.
a) Bestimmen Sie eine Koordinatengleichung der Ebene E.
Begründen Sie, dass es sich bei dem Viereck QRST um ein Trapez handelt.
Berechnen Sie den Flächeninhalt des Trapezes QRST.
(Teilergebnis: E: -x1+2x2+2x3=22)
(6 VP)
b) Der kleine Teilkörper wird mit den Schnittkanten nach unten auf den großen Teilkörper gestellt.Bestimmen Sie die Höhe des zusammengesetzten Körpers.
(1,5 VP)
c) Der Container besitzt eine Tür, die im geschlossenen Zustand durch das Viereck ODAF dargestellt wird. Die Tür ist drehbar um die Kante, die durch die Strecke OD beschrieben wird.Jede Ebene Ta: ax1+x2=0; a≥0 beschreibt eine mögliche Stellung dieser Tür.
Bestimmen Sie den Wert für a, für den der Öffnungswinkel der Tür 30° beträgt.
(2,5 VP)